1.归一化

我们用一组数据在每一步进行相应处理来演示这个完整的过程：
原始样本：([10, 12, 9, 15, 14])，样本数 (N=5)

[mu = frac{10 + 12 + 9 + 15 + 14}{5} = frac{60}{5} = 12.0 ]

（2）计算每个样本与均值的差 ((x - mu)) 以及平方差

（3）计算方差与标准差

总体方差（分母使用 (N)）：

[sigma^2 = frac{1}{N}sum_{i=1}^{N}(x_i-mu)^2 = frac{26}{5} = 5.2 ]

总体标准差：

[sigma = sqrt{sigma^2} = sqrt{5.2} approx 2.280351 ]

（4）执行标准化变换

每个样本的标准化结果：

[z = frac{x - mu}{sigma} ]

逐项计算：

因此标准化后的结果为：

[[-0.877058, 0.0, -1.315587, 1.315587, 0.877058] ]

这样，我们就对数据完成了一次标准化，那进行这些步骤的作用又是什么呢？

1.2标准化的作用

我们来看一下各个步骤后，样本数据的变化：

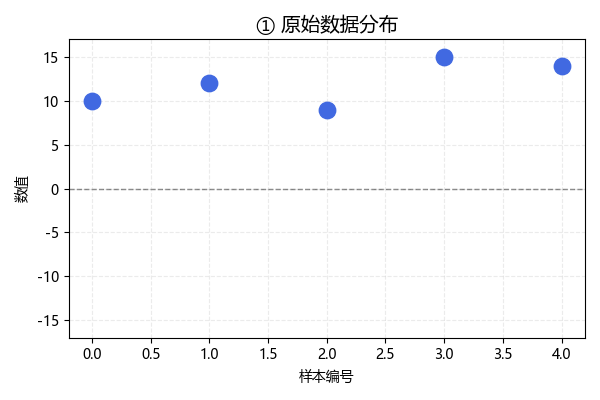
这是未经处理的原始数据，现在，我们按照标准化公式一步步进行：

[z = frac{x - mu}{sigma} ]

将各数据减去均值，这一步也叫做中心化，此时数据分布如下：

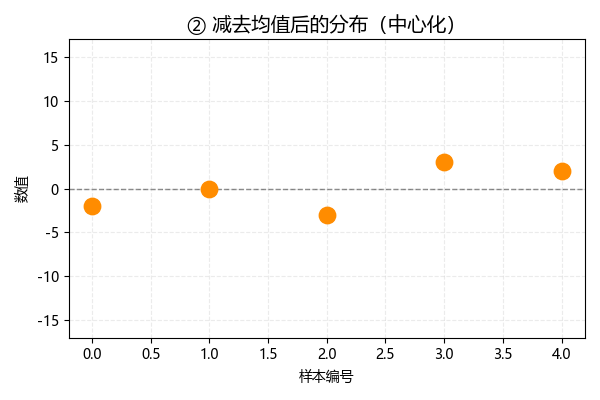
可以发现，中心化后，数据的均值变为 0：

[ frac{1}{N}sum_{i=1}^{N} z_i = 0 ]

现在，我们再把中心化的数据除以标准差，此时数据分布如下：

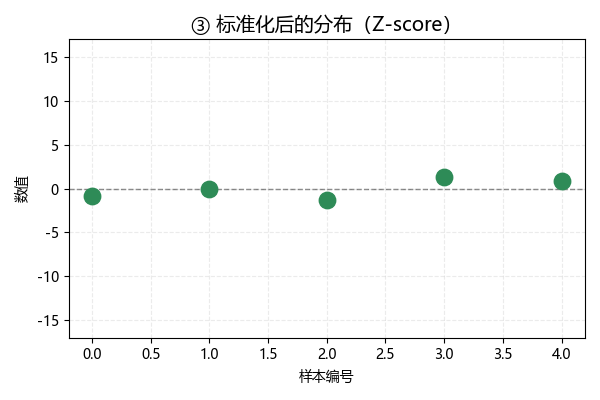
经过这一步，标准化后数据的标准差为 1：

[sqrt{frac{1}{N}sum_{i=1}^{N}(z_i - 0)^2} = 1 ]

也就是说，标准化后，数据的均值变为0，标准差变为1，这是它的作用，可这样的变换又是如何帮助训练的呢？
我们继续下一节。

1.3 标准化如何帮助训练？

（1）消除量纲差距的同时保持特征信息

在现实数据中，不同特征往往有不同的单位或数量级。
例如，在一个房价预测模型中：

• 房屋面积以“平方米”计，数值可能在几十到几百；
• 房间数量只在“1~5”之间变化。
  如果不做标准化，面积特征的值远大于房间数，模型在更新参数时会更偏向面积，而忽视房间数量的影响。

对此，标准化这样解决这个问题：

• 中心化：将每个特征的均值移动到 0，使数据以 0 为中心，正负对称，方便神经网络处理。
• 除以标准差：标准差就像一个“伸缩尺”，根据特征自身的波动范围对数据进行拉伸或压缩，波动大的特征被压缩幅度大，波动小的特征被压缩幅度小，从而统一特征尺度。
  要说明的是，除以标准差精妙的地方在于统一尺度的同时保留了同一特征内的差距。

举个例子：
对于两个人的年龄，一个人20岁，一个人10岁。
压缩后，前一个人变成了2岁，后一个人变成了1岁。
但是他们之间的差别关系没有变化，前者仍比后者大，我们只是把跨度从10岁缩小从了1岁来减少波动性。模型依旧可以区分两个样本的差别。

我们再用房屋的实例说明来整体演示一下：

1. 设房屋面积原始值：[50, 120, 200, 300, 400]， 房间数原始值：[1, 2, 3, 4, 5]
2. 中心化后：面积：[−167, −97, −17, 83, 183]，房间数：[−2, −1, 0, 1, 2]
3. 除以标准差（面积 σ≈145.44，房间数 σ≈1.414）后： 面积标准化：[−1.15, −0.67, −0.12, 0.57, 1.26]， 房间数标准化：[−1.41, −0.71, 0, 0.71, 1.41]
   这样，通过标准化，面积和房间数都被缩放到大致相似的范围，梯度更新时影响力平衡，同时保持了各房屋之间的相对差异。
   可以形象地理解为：每个特征都被配上了“统一的尺子”，让它们在同一尺度下公平竞争，既消除了量纲差距，又保持原始信息。

（2）平衡含正负值的数据集

标准化后的数据以 0 为中心，分布更对称，特别适合使用如 tanh、ReLU 等激活函数的神经网络。
我们用tanh举例：

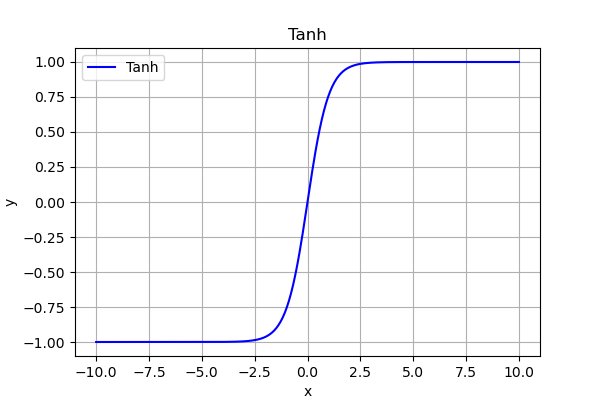
如果输入特征全是正数，tanh 的输出始终偏向 1 区域，梯度几乎为 0，学习停滞。
而经过标准化后，输入既有正又有负，输出能覆盖整个区间，梯度保持活跃，网络学习更充分。

这便是关于归一化的内容，下一篇便是本周理论部分的最后一篇，是关于网络运行中一些常见的梯度现象和其应对方法。