梯度稍微变小了一点，这没问题。
但如果层数再多，比如 20 层：

[text{总梯度} = 0.9^{20} = 0.12 ]

这时梯度几乎消失了。
如果再更多层呢？这样下来，每次参数的更新就会小的几乎没有，就像一个步履蹒跚的老人下山，让模型的学习永无尽头，这就是梯度消失（vanishing gradient）。
反过来，如果每层平均值是 1.2：

[1.2^{20} = 38.3 ]

这时梯度变得极大，出现“爆炸”，这样次次迭代后参数就会像一个超人一样次次进化，最后飞在天上下不来，更别说“找谷底”了，这就是梯度爆炸(Exploding Gradient)。

再用一个例子来说明二者在实际运行中的效果：

• 梯度消失：像一连串传话游戏，传到最后只剩耳语，网络“听不见”误差信号。
• 梯度爆炸：像一连串扩音器，每层都加倍音量，最后系统崩溃。

再来看一个实例：
假设现在我们使用 Sigmoid 激活函数：

[sigma(x) = frac{1}{1 + e^{-x}} ]

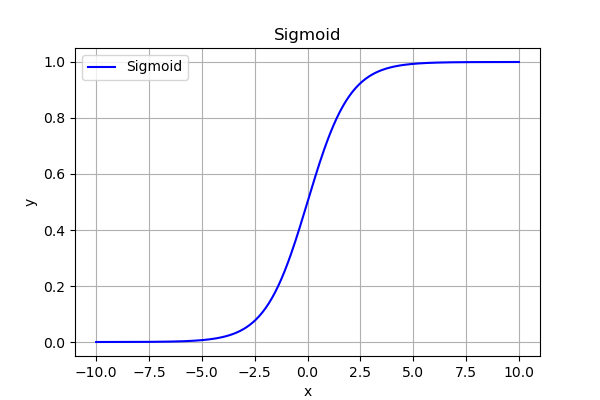
其导数最大值为 (0.25)。
如果网络有 10 层，那么误差信号传回输入层的幅度最多为：

[(0.25)^{10} = 9.5 times 10^{-7} ]

几乎为零。
这就是为什么深层网络用 Sigmoid 会难以训练，我们通常在二分类的输出层使用它而不是隐藏层的原因之一。

最后总结一下判断二者的实验现象：

• 梯度消失：loss 几乎不下降，权重几乎不变。
• 梯度爆炸：loss 一直 NaN (not a number) 或突然发散（突然急剧增加）。

而如何避免这种情况产生？很明显，在数据合理的前提下，我们就要给参数一个合理的初值，让它在后续更新中既不会太大，也不会太小。
也就是初始化问题，之前在简单的神经网络里，我们学习了随机初始化，而现在深层神经网络中，我们也有相应的初始化方法。

1.2 应对二者的权重初始化

梯度之所以不稳定，是因为初始权重太小或太大导致信号在层间放大或缩小。
因此我们希望每一层的输入和输出方差保持一致。
好像有些模糊，为什么方差一致就能让梯度稳定？ 我们由此来展开解释：

（1）什么叫“方差一致”？

在神经网络中，每一层都会对输入做一次线性变换,看一眼老公式，就不再重复了：

[z^{(l)} = W^{(l)}x^{(l-1)} + b^{(l)} ]

而现在，我们希望：

[Var(z^{(l)}) approx Var(x^{(l-1)}) (Var：方差，variance) ]

也就是说，一层输出的波动幅度（方差）不要比输入大或小太多。

（2）为什么方差变化会出问题？

其实这和我们刚刚阐述的梯度现象是一个道理，只是刚刚是用反向传播说明，现在是用正向传播说明：
想象每层都稍微放大一点信号（方差增加）：

[Var(x^{(l)}) = 1.2 times Var(x^{(l-1)}) ]

如果有 20 层：

[Var(x^{(20)}) = 1.2^{20} times Var(x^{(0)}) approx 38 times Var(x^{(0)}) ]

这意味着信号在传播过程中被放大了 38 倍，
→ 在反向传播时，梯度也会被同样放大 → 梯度爆炸。
反过来，如果每层都缩小一点信号（方差减少）：

[Var(x^{(l)}) = 0.9 times Var(x^{(l-1)}) ]

那么：

[Var(x^{(20)}) = 0.9^{20} times Var(x^{(0)}) approx 0.12 times Var(x^{(0)}) ]

→ 信号越来越小，最终接近 0，
→ 梯度反向传播时也会逐层消失 → 梯度消失。

还是刚刚那个比方：

• 如果每层都“放大”一点，信号越传越响亮，最后炸麦 → 梯度爆炸；
• 如果每层都“削弱”一点，信号越传越轻，最后听不见 → 梯度消失；
• 只有音量稳定传递，才能让整首歌（网络）正常演奏完。
  

因此，我们才需要每一层的输入和输出方差保持一致。

（3）这和权重初始化的关系

理清楚逻辑后，我们来看看如何通过初始化来实现方差一致：
对于单个神经元：（偏置不影响方差，这里省去）

[z = sum_{i=1}^n w_i x_i ]

假设：

• 每个 (x_i) 均值为 0，方差为 (Var(x_i)=sigma_x^2)；
• 权重 (w_i) 独立同分布，方差为 (Var(w_i)=sigma_w^2)。
  在这些假设下，线性组合的方差是各项方差之和：

[Var(z) = sum_{i=1}^n Var(w_i x_i) ]

又因为 (w_i) 与 (x_i) 独立：（这是数学里概率论部分的知识）

[Var(w_i x_i) = Var(w_i),Var(x_i) = sigma_w^2 sigma_x^2 ]

因此：

[Var(z) = n ,sigma_w^2 sigma_x^2 ]

若我们希望输出的方差与输入的方差相同（即方差保持一致），设 (Var(z) = sigma_x^2)，则：

[n ,sigma_w^2 sigma_x^2 = sigma_x^2 quadRightarrowquad sigma_w^2 = frac{1}{n} ]

最终，我们得出结论：如果输入方差为 (sigma_x^2) 且满足上述独立性假设，那么把权重的方差设为 (1/n)（(n) 为该层的输入维度，也称 fan_in）可以使输出方差与输入方差保持一致。

来看一个具体的例子:

假设 fan_in = n = 100，且输入每个通道方差 (sigma_x^2 = 1)（应用归一化的结果）。

• 由公式得到(sigma_w^2 = 1/n = 1/100 = 0.01)
• 那么输出方差： (Var(z) = n sigma_w^2 sigma_x^2 = 100 times 0.01 times 1 = 1)，与输入方差相等（方差一致）。

若不这么做，比如 (sigma_w = 0.5)（(sigma_w^2=0.25)）更大：

• 输出方差 (=100 times 0.25 times 1 = 25) → 被放大 25 倍（梯度爆炸）。

若 (sigma_w = 0.01)（(sigma_w^2=1e-4)）更小：

• 输出方差 (=100 times 1e-4 = 0.01) → 被缩小（梯度消失）。

这便是权重初始化的核心概念：即通过控制权重的方差，让信号方差保持恒定。 既避免了梯度爆炸，又避免了梯度消失。

在此思想上，便发展出了以下几种适应不同激活函数的初始化，涉及具体实验和文献，就不再展开了：

总结一下，把权重初始化为合适的方差，相当于在网络刚开始训练时把“信号音量”调到合适的档位，这能让信号在层间既不被放大成噪音（爆炸），也不被削弱成耳语（消失）。不同激活函数会改变信号统计特性，所以需要不同的初始化。

2.梯度检验（Gradient Checking）

梯度检验的目标是验证反向传播计算的梯度是否正确。
这在早期手写反向传播时代是非常重要的调试工具。

梯度检验的核心思想是：用数值方法逼近梯度，再与反向传播计算的梯度对比，检查实现是否正确,我们用实例来更好的说明这个过程。

2.1计算数值梯度

首先，假设损失函数为：(J(theta) = theta^2)
当前参数：(theta = 3)
然后，用有限差分法近似梯度：

[frac{partial J(theta)}{partial theta} approx frac{J(theta + varepsilon) - J(theta - varepsilon)}{2varepsilon}, quad varepsilon = 10^{-4} ]

计算：

[J(3 + 0.0001) = 9.00060001 ,J(3 - 0.0001) = 8.99940001 ]

[grad_{num}= frac{9.00060001 - 8.99940001}{0.0002} = 6.000 ]

现在我们就得到了数值梯度，这是我们用有限差分计算得到的实际数值。

2.2 计算理论梯度

现在，对损失函数求导代入：

[grad_{bp}=frac{dJ}{dtheta} = 2theta = 6 ]

现在我们就得到了理论梯度，这是我们通过求导得到的理论答案。

2.3 进行梯度检验

梯度检验的公式如下：

[error = frac{|grad_{num} - grad_{bp}|}{|grad_{num}| + |grad_{bp}|} = frac{|6.000 - 6|}{6.000 + 6} =0 ]

结果为 (0)，说明反向传播梯度实现正确，但实际上的数值不会这么简单。
若我们的反向传播错误（例如少乘了一项），数值梯度与反向传播梯度之间的差异就会很明显，从而发现问题。
对梯度检验的结果判别如下：

这便是早期梯度检验的主要过程，但在现在已经很少使用了。

2.4 实际运用中要注意的点

在实际使用梯度检验时，需要注意以下几点：

1. 梯度检验不用于训练
   • 梯度检验的目的是验证反向传播实现是否正确，并不是训练算法本身。
   • 它通常只在模型开发阶段使用，一旦确认实现正确，就可以关闭，以免浪费计算资源。
2. 梯度检验和 Dropout/正则化一般不一起使用
   • Dropout 操作会引入随机性，会导致数值梯度和反向传播梯度不完全一致。
   • 为了保证梯度检验结果准确，通常需要在 关闭 Dropout 的训练模式 下进行。

3.”人话版“总结