在前文中我们使用的损失函数都是均方误差（MSE，Mean Squared Error），本篇介绍一些其他的损失函数形式，以及他们的不同用途。

1. 回归任务常用损失函数

1.1 均方误差（MSE, Mean Squared Error）

均方误差（MSE）是回归任务中最常用的损失函数之一，用于衡量模型预测值与真实值之间的平均平方差异。其核心思想是通过平方放大较大误差的影响，从而驱动模型更关注预测偏差较大的样本。

其中，(y_i​)为真实值， (hat{y_​i}​)为预测值，N为样本数量。

平方项的作用：

• 消除正负符号影响：无论预测值大于还是小于真实值，误差的平方均为正数，避免正负误差相互抵消。
• 放大较大误差的惩罚：平方操作使大误差的损失呈二次增长，例如误差为 2 时损失为 4，误差为 3 时损失为 9，模型会更关注减少大误差。

函数特性：

• 凸性 MSE 是凸函数，保证梯度下降法能收敛到全局最优解（前提是学习率合理）。
• 光滑可导 平方函数处处连续可导，适合梯度下降等优化算法。

梯度计算：

• 对预测值的梯度为：
  

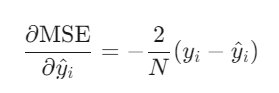
• 梯度与误差成正比，误差越大，参数更新幅度越大。

计算效率 ：

• 公式简单，适合大规模数据。

对异常值的敏感度：

• 非鲁棒性 平方操作会显著放大异常值的损失，导致模型过度拟合异常点

适用场景：

• 数据分布相对均匀、异常值较少且需快速收敛的模型训练。

1.2 平均绝对误差（MAE, Mean Absolute Error）

平均绝对误差（Mean Absolute Error, MAE）是回归任务中衡量预测值与真实值偏差的核心指标，其数学表达式为：

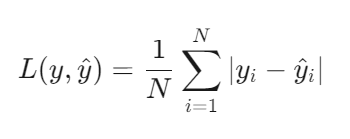
其中，(y_i​)为真实值， (hat{y_​i}​)为预测值，N为样本数量。

绝对值的作用：

• 消除正负误差抵消：直接取绝对值避免了正负误差相加导致的总误差低估问题（如误差为+1和-1时，未取绝对值则总误差为0，但实际存在偏差）
• 直观反映误差量级：绝对值保留了误差的实际大小，便于直接理解预测偏差的物理意义（如房价预测中MAE的单位为“美元”）

函数特性：
凸性： MAE是凸函数，保证优化过程中存在全局最优解。
不可导性： 绝对值函数在零点不可导，导致梯度下降法需采用次梯度（如符号函数）或平滑近似（如Huber损失）进行优化。

梯度计算：

• 非零点梯度为常数±1，导致参数更新步长固定，收敛速度较慢。
• 对比MSE（梯度与误差成正比），MAE对大误差的惩罚力度较小，优化过程更稳定但可能陷入局部最优

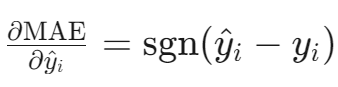
计算效率 ：

• 时间复杂度低：仅需线性遍历计算绝对值和均值，复杂度为O(n)，适用于大规模数据集
• 硬件友好：无平方运算，内存占用少，适合嵌入式系统或实时预测场景

对异常值的敏感度：

• 低敏感性：MAE对异常值的鲁棒性强于MSE，因误差未被平方放大。例如，若某样本误差为10，MAE贡献为10，而MSE贡献为100 。

适用场景：

• 异常值较多的数据，需直观解释误差的场景，实时性要求高的系统

1.3 Huber Loss

Huber Loss 是一种结合了 均方误差（MSE） 和 平均绝对误差（MAE） 优点的损失函数，由统计学家 Peter Huber 提出，主要用于回归任务。其核心思想是：对小误差使用平方惩罚（类似 MSE），对大误差使用线性惩罚（类似 MAE），从而在异常值鲁棒性和优化效率之间取得平衡。

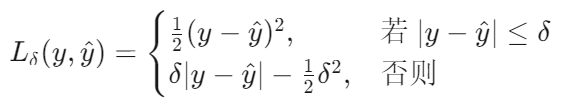
其中：

• y 是真实值，y^​ 是模型预测值。
• δ 是阈值参数，需手动设定（通常取 1.0 或通过数据分布调整）。

函数特性：
这是一个分段函数，当我们将∣y−y^​∣= δ代入这两个式子，可以得出它在∣y−y^​∣= δ时连续且可导。
(1) 对小误差的平方惩罚（MSE 特性）
当预测误差 ∣y−y^​∣≤δ 时，Huber Loss 退化为 均方误差（MSE） 的一半：

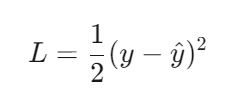
(2) 对大误差的线性惩罚（MAE 特性）
当预测误差 ∣y−y^​∣>δ 时，Huber Loss 退化为 线性损失：

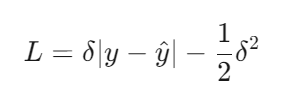
(3) 平滑过渡的关键设计

• 阈值 δ：控制从平方损失到线性损失的切换点。
  • δ 越小，Huber Loss 越接近 MSE（对异常值敏感）。
  • δ 越大，Huber Loss 越接近 MAE（对异常值鲁棒）。

梯度计算：
Huber Loss 的梯度计算如下：

• 小误差时：梯度与误差成正比，类似 MSE，参数更新幅度与误差大小相关。
• 大误差时：梯度固定为 ±δ，类似 MAE，避免梯度爆炸。

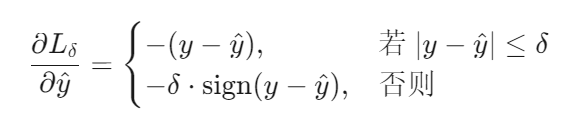
适用场景：

• 异常值较多的回归任务，需要平衡精度与鲁棒性的场景，实时系统或嵌入式设备。

2 分类任务常用损失函数

2.1 交叉熵损失（Cross-Entropy Loss）

交叉熵损失函数（Cross-Entropy Loss）是分类任务中最核心的损失函数之一，用于衡量模型预测概率分布与真实标签分布之间的差异。其核心思想基于信息论中的交叉熵概念，通过最小化两个分布的差异来优化模型参数。

公式（二分类）：

多分类扩展（Softmax + Cross-Entropy）：

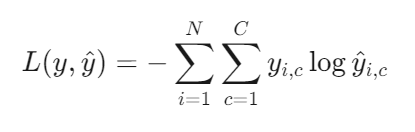
二分类问题中，我们通常用sigmoid函数输出最终结果，其真实值为0或1。从公式中可以看出，当真实值为0时，[ ]内保留了后一项，衡量与0之间的误差；当真实值为1时，[]内保留了前一项，衡量与1之间的误差。

多分类问题中，通常用Softmax函数输出最终结果，而多分类标签通常采用one-hot编码，也就是只有真实分类对应的元素为1，其他为0。由于Softmax函数特性，输出各元素之间是联动的，我们只需关注真实分类所对应的预测误差即可。从公式中可知，如果真实分类为c=3，那么one-hot编码中只有c=3对应的(y_i)为1，即(y_{i,3}=1)，其他的(y_{i,p}=0) where p ≠ 3 。那么公式中第二层求和项只剩下c=3这一项。也就是只剩下真是分类所对应的预测误差。

为什么也没有二分类中的 ((1-y_i)log(1-hat{y_i})) 这一项了？
因为真实分类下对应的(y_i)为1，这一项也为0。

与MSE的对比
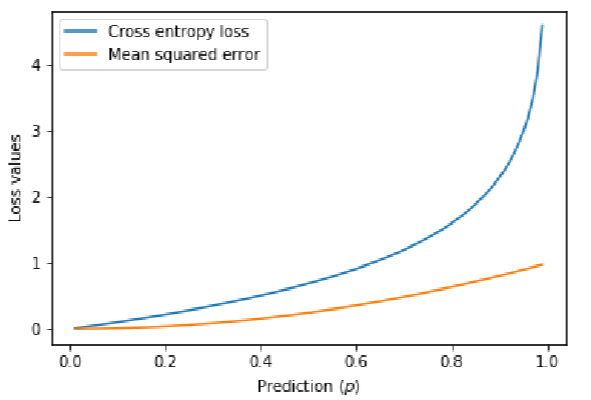
下图为真实值y=0时，交叉熵损失和MSE的对比，从图中可以看到，交叉熵损失的误差惩罚更高，而且随着误差增加，其惩罚的增量更多，迫使模型快速修正错误。这有助于快速的收敛。

适用场景：
多标签分类（互斥类别）
输出层Softmax激活，计算多分类交叉熵损失，如：MNIST 手写数字识别（每张图片仅属于一个数字类别）。
多标签分类（非互斥类别）
每个类别独立使用 Sigmoid 激活，逐类别计算二分类交叉熵后求和，如：图像中同时包含“猫”和“狗”的情况。