在数据分析的世界里， “距离” 不仅仅是地图上两点之间的路程。

距离 ，本质上是衡量两个事物 “相似度” 的尺子。

• 距离越近 = 相似度越高
• 距离越远 = 差异越大

如果你想做用户画像聚类、想做商品推荐系统，或者想识别信用卡欺诈交易，你首先要选对这把“尺子”。

本文将带你全面了解数据分析中常用的各种距离度量，从最直观的欧氏距离到复杂的时间序列距离。

为了方便理解，我将它们分为了五大门派。

1. 第一门派：几何空间的测量者

这一类距离最符合我们的直觉，通常用于处理数值型数据（比如身高、体重、经纬度）。

1.1. 欧氏距离：最直观的“直线距离”

欧氏距离就是我们常说的 “直线距离”。

在二维平面上，两点间的欧氏距离就是连接它们的直线长度。

应用场景：

• 外卖配送： 假设你是无人机送外卖，不受道路限制，直接飞过去，这就是欧氏距离。
• K-Means 聚类： 最常用的距离度量。

代码示例：

import numpy as np
# 后面的代码示例多次用到 distance，不再重复引用了
from scipy.spatial import distance

# 两个用户的特征：[活跃时长(小时), 消费金额(元)]
user_A = [2.5, 300]
user_B = [3.0, 350]

d_euclidean = distance.euclidean(user_A, user_B)
print(f"欧氏距离: {d_euclidean:.2f}")

# 运行结果：
'''
欧氏距离: 50.00
'''

图形化效果如下：

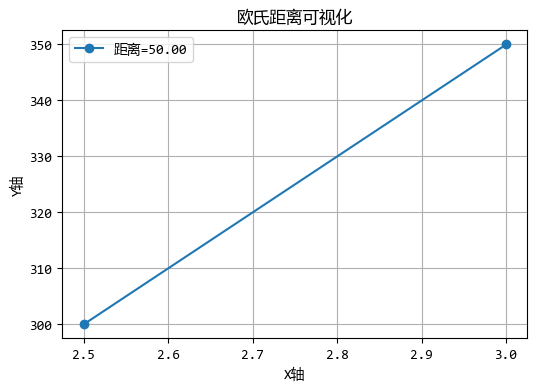
注意：欧氏距离对数据的尺度敏感！如果特征的单位不同（如年龄和收入），直接计算会导致收入特征主导距离计算。

1.2. 曼哈顿距离：城市街区的走法

想象在纽约曼哈顿的街道上行走，你不能斜穿大楼，只能沿着街道走。曼哈顿距离就是这种 “城市街区距离”。

应用场景：

• 城市物流： 真实的快递员配送路径估算。
• 高维数据： 在某些高维数据中，曼哈顿距离比欧氏距离更能抗干扰（Robust）。

代码示例：

# 外卖配送示例：从餐厅到顾客的路径
restaurant = np.array([3, 7])  # 坐标(3,7)
customer = np.array([8, 2])  # 坐标(8,2)

euclidean = distance.euclidean(restaurant, customer)
manhattan = distance.cityblock(restaurant, customer)

print(f"餐厅到顾客的直线距离（欧氏）: {euclidean:.2f}")
print(f"餐厅到顾客的街区距离（曼哈顿）: {manhattan:.2f}")

# 运行结果：
'''
餐厅到顾客的直线距离（欧氏）: 7.07
餐厅到顾客的街区距离（曼哈顿）: 10.00
'''

1.3. 切比雪夫距离：棋盘上的王者

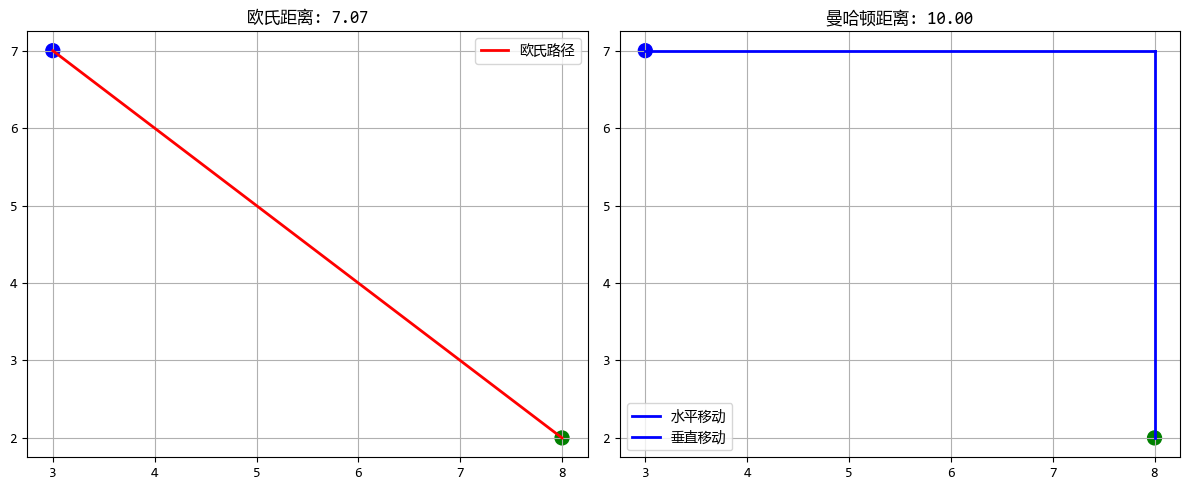
也就是国际象棋中“国王”移动的步数。国王可以横着走、竖着走，也能斜着走，且步数都算 1。

它只在乎数值差最大的那个维度。

应用场景：

• 仓储物流： 龙门吊抓取货物，横向移动和纵向移动可以同时进行，时间取决于最远的那个方向。

代码示例：

d_chebyshev = distance.chebyshev(user_A, user_B)
print(f"切比雪夫距离: {d_chebyshev:.2f}")

1.4. 闵可夫斯基距离：距离的通用公式

它是上面三种距离的“爸爸”。通过一个参数 p 来控制：

• 当 p=1 时，就是曼哈顿距离。
• 当 p=2 时，就是欧氏距离。
• 当 p=∞ 时，就是切比雪夫距离。

应用场景： 当你不确定用哪种几何距离时，可以调节 p 值来寻找最优解。

代码示例：

# 对比不同p值的效果
point1 = np.array([0, 0])
point2 = np.array([3, 4])

p_values = [1, 2, 3, 5, 10]
distances = []

for p in p_values:
    dist = distance.minkowski(point1, point2, p)
    distances.append(dist)
    print(f"p={p}: 距离={dist:.2f}")

# 运行结果：
'''
p=1: 距离=7.00
p=2: 距离=5.00
p=3: 距离=4.50
p=5: 距离=4.17
p=10: 距离=4.02
'''

2. 第二门派：方向与相关性的探索者

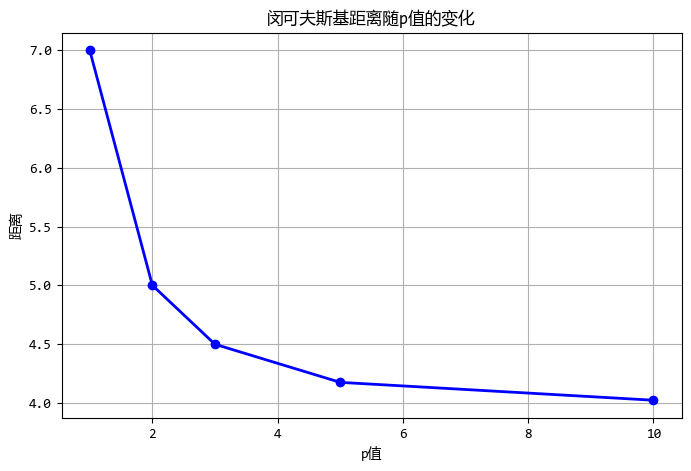
这一类距离不关心 “数值大小”，更关心 “趋势方向” 或 “统计关系”。

2.1. 余弦距离：关注方向而非大小

余弦距离衡量的是两个向量方向的差异，而不是它们的大小差异。

这在文本分析中特别有用，因为文档的长度不同，但主题可能相似。

应用场景：

• 文本相似度（热点）： 比如比较两篇文章。文章 A 只有 100 字，文章 B 有 10000 字，虽然词频数值差很大，但如果它们都在讲“人工智能”，它们的方向（角度）是一致的。
• 推荐系统： 用户打分偏好。

代码示例：（用几个简单的新闻标题来计算余弦相似度）

# 文本向量（假设是词频）：[AI, 苹果, 股票]
doc_1 = [10, 0, 5]  # 科技财经文
doc_2 = [20, 0, 10] # 长篇科技财经文（方向一致）
doc_3 = [0, 10, 0]  # 水果文

# 余弦距离 = 1 - 余弦相似度
# 接近0，表示非常相似
print(f"同类文章余弦距离: {distance.cosine(doc_1, doc_2):.2f}")

# 接近1，表示无关
print(f"不同类文章余弦距离: {distance.cosine(doc_1, doc_3):.2f}")

# 运行结果：
'''
同类文章余弦距离: 0.00
不同类文章余弦距离: 1.00
'''

2.2. 相关系数距离：衡量线性关系

基于皮尔逊相关系数的距离，衡量两个变量之间线性相关性的差异。

应用场景：

• 股票分析： 衡量两只股票的走势是否同步。如果一支涨另一支也涨，它们的相关距离就很小，哪怕一个股价是 10 元，另一个是 1000 元。

# 两只股票过去5天的涨跌幅
stock_A = [0.1, -0.2, 0.3, 0.1, 0.0]
stock_B = [0.2, -0.4, 0.6, 0.2, 0.0] # 走势完全也就是2倍关系

d_correlation = distance.correlation(stock_A, stock_B)
print(f"相关系数距离: {d_correlation:.2f}")

# 运行结果
'''
相关系数距离: 0.00
'''

可以尝试调整调整stock_A和stock_B的数值，再看看相关系数的变化。

2.3. 马氏距离：考虑数据分布的距离

马氏距离考虑了数据的协方差结构，是一种尺度无关且排除了特征相关性的距离度量。

应用场景：

• 异常检测： 假设你统计人的身高和体重。如果你用欧氏距离，一个 190cm、50kg 的人可能离中心点不远。但考虑到身高体重的正相关性（高的人通常重），这个数据点在马氏距离下就会非常远（非常异常）。

# 需要先计算协方差矩阵的逆
np.random.seed(42)
height = np.random.normal(170, 10, 20)  # 20个身高样本
weight = height * 0.5 + np.random.normal(0, 5, 20)  # 体重与身高相关
data = np.column_stack([height, weight])

cov_matrix = np.cov(data.T)
inv_cov_matrix = np.linalg.inv(cov_matrix)

point_1 = [170, 60] # 正常点
point_2 = [190, 50] # 异常点（又高又瘦）

d_mah_1 = distance.mahalanobis(point_1, np.mean(data, axis=0), inv_cov_matrix)
d_mah_2 = distance.mahalanobis(point_2, np.mean(data, axis=0), inv_cov_matrix)

print(f"正常点马氏距离: {d_mah_1:.2f}")
print(f"异常点马氏距离: {d_mah_2:.2f}") # 距离会很大

# 运行结果：
'''
正常点马氏距离: 4.93
异常点马氏距离: 9.06
'''

3. 第三门派：集合与分类的裁判

当数据不是数字，而是分类、标签或字符串时，我们用这些。

3.1. 杰卡德距离：集合的相似度

杰卡德距离衡量两个集合的差异程度，通过计算交集与并集的比例得到。

应用场景：

• 电商推荐： 用户 A 买了 {苹果, 香蕉}，用户 B 买了 {苹果, 香蕉, 西瓜}。通过杰卡德距离计算他们的购买重合度，进而推荐商品。

d_jaccard = distance.jaccard([1, 1, 0], [1, 1, 1]) # boolean vector
print(f"杰卡德距离: {d_jaccard:.2f}")

# 运行结果：
'''
杰卡德距离: 0.33
'''

3.2. 汉明距离：字符串的差异度量

汉明距离衡量两个等长字符串在对应位置上不同字符的数量。

应用场景：

• 拼写纠错： "banana" 和 "banane"，只有一个字母不同，汉明距离为 1。
• 信息编码： 通信中检测数据传输是否出错。

d_hamming = distance.hamming([1, 0, 1], [1, 0, 0])
print(f"汉明距离: {d_hamming:.2f}") # 输出比例，有些库输出个数

# 运行结果：
'''
汉明距离: 0.33
'''

3.3. 编辑距离：字符串转换的代价

编辑距离（Levenshtein距离）衡量将一个字符串转换为另一个字符串所需的最少单字符编辑操作次数（插入、删除、替换）。

应用场景：

• 搜索引擎： 你输错单词时，百度/谷歌提示“您是不是要找...”，就是通过编辑距离找到最接近的正确词。

# 注：标准库无此函数，通常用 pip install Levenshtein 或自定义
# 这里用简单的逻辑演示概念
def simple_levenshtein(s1, s2):
    if len(s1) 

4. 第四门派：分布差异的鉴定师

用于衡量两个“概率分布”（比如两个直方图）有多像。这在机器学习和生成式 AI 中非常火。

4.1. KL 散度：衡量概率分布差异

KL散度衡量一个概率分布与另一个参考分布之间的差异，但不是对称的。

应用场景：

• 机器学习训练： 衡量模型预测的概率分布与真实标签分布之间的差异（Loss Function）。

from scipy.stats import entropy
p = [0.1, 0.9] # 真实分布
q = [0.2, 0.8] # 预测分布
kl_div = entropy(p, q)
print(f"KL散度: {kl_div:.4f}")

# 运行结果：
'''
KL散度: 0.0367
'''

4.2. JS 散度：衡量概率分布差异-对称

JS散度是KL散度的对称版本，值域固定。

应用场景：

• GAN (生成对抗网络)： 早期用于衡量生成图片分布与真实图片分布的相似度。

d_js = distance.jensenshannon(p, q)
print(f"JS散度: {d_js:.4f}")

# 运行结果：
'''
JS散度: 0.0998
'''

4.3. Wasserstein 距离：地球搬运距离

Wasserstein距离衡量将一个概率分布"搬运"成另一个所需的最小工作量，直观理解是将一堆沙子变成指定形状所需的最小移动距离。

应用场景：

• 图像生成 (WGAN)： 即使两个分布完全不重叠（KL 散度会失效），Wasserstein 距离也能给出合理的数值，指导 AI 学习。

from scipy.stats import wasserstein_distance
d_wasserstein = wasserstein_distance([0, 1, 3], [5, 6, 8])
print(f"Wasserstein距离: {d_wasserstein:.2f}")

# 运行结果：
'''
Wasserstein距离: 5.00
'''

5. 第五门派：时间序列的变形者

5.1. DTW 距离：时间序列的弹性匹配

动态时间规整（DTW）距离允许时间轴伸缩弯曲，用于衡量两个时间序列的相似性，即使它们在时间轴上不完全对齐。

应用场景：

• 语音识别/股票分析： 两个人读同一个单词 "Hello"。
  • 人 A：H-e-l-l-o (语速快)
  • 人 B：H-e-e-e-l-l-o-o (语速慢)
  • 欧氏距离会认为这完全不同，但 DTW 会把时间轴“对齐”，发现它们其实很像。

# 简单的DTW概念代码（实际应用推荐使用 fastdtw 库）
from scipy.spatial.distance import euclidean

def dtw_distance(s1, s2):
    n, m = len(s1), len(s2)
    dtw_matrix = np.zeros((n+1, m+1))
    dtw_matrix[0, 1:] = np.inf
    dtw_matrix[1:, 0] = np.inf

    for i in range(1, n+1):
        for j in range(1, m+1):
            cost = abs(s1[i-1] - s2[j-1])
            dtw_matrix[i, j] = cost + min(dtw_matrix[i-1, j],    # 插入
                                          dtw_matrix[i, j-1],    # 删除
                                          dtw_matrix[i-1, j-1])  # 匹配
    return dtw_matrix[n, m]

ts_1 = [1, 2, 3, 4]
ts_2 = [1, 1, 2, 3, 4, 4] # 同样趋势，但多了重复（慢动作）
print(f"DTW距离: {dtw_distance(ts_1, ts_2)}")

# 运行结果：
'''
DTW距离: 0.0
'''

6. 总结：如何选择你的“尺子”？

面对新数据，别盲目选欧氏距离，参考下面的建议：

1. 普通数值数据，看绝对大小： 选 欧氏 或 曼哈顿。
2. 看重方向/喜好，忽略绝对数值： 选 余弦距离（如文本、推荐）。
3. 看重趋势变化，忽略数值大小： 选 相关系数距离（如股票）。
4. 数据相关性强，且有离群点： 选 马氏距离。
5. 集合、标签类数据： 选 杰卡德 或 汉明。
6. 概率分布对比（AI 模型）： 选 KL 或 Wasserstein。
7. 长短不一的时间序列： 选 DTW。

文中代码中大部分的距离关键是掌握其概念和应用场景，至于其距离算法的实现，scipy库中大部分都有封装好的函数，即使没有，也可以用其他库来代替。